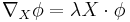Killing spinor

Killing spinor is a term used in mathematics and physics. By the more narrow definition, commonly used in mathematics, the term Killing spinor indicates those twistor spinors which are also eigenspinors of the Dirac operator, see Th. Friedrich , "Der erste Eigenwert des Dirac Operators einer kompakten, Riemannschen Mannigfaltigkeit nichtnegativer Skalarkrümmung", Math. Nachr. 97 (1980), 117-146. The term is named after Wilhelm Killing.

Another equivalent definition is that Killing spinors are the solutions to the Killing equation for a so-called Killing number.

More formally:

A Killing spinor on a manifold M is a spinor field $\phi$ which satisfies

$\nabla_X\phi=\lambda X\cdot\phi$

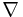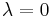for all tangent vectors X, where $\nabla$ is the spinor covariant derivative, $\cdot$ is Clifford multiplication and $\lambda$ is a constant, called the Killing number. If $\lambda=0$ then the spinor is called a parallel spinor.

In physics, Killing spinors are used in supergravity and superstring theory, in particular for finding solutions which preserve some supersymmetry. They are a special kind of spinor field related to Killing vector fields and Killing tensors.

Killing spinor

External links